Representing complex data
We’ve seen:
base types:
Bool,Int,Integer,Floatsome ways to build up types: given types
T1, T2- functions:
T1 -> T2 - tuples:
(T1, T2) - lists:
[T1]
- functions:
Algebraic Data Types: a single, powerful technique for building up types to represent complex data
- lets you define your own data types
- subsumes tuples and lists!
Algebraic Data Types
Type Synonyms: naming existing types
Product Types: bundling things together
Sum Types: types with multiple variants
Recursive Types: types that contain themselves
Polymorphic Datatypes: datatypes with parameters
Type Synonyms
Synonyms are just names (“aliases”) for existing types
- think
typedefinC
A type to represent circles
A tuple (x, y, r) is a circle with center at (x, y) and radius r
type CircleT = (Double, Double, Double)
A type to represent cuboids
A tuple (length, depth, height) is a cuboid
type CuboidT = (Double, Double, Double)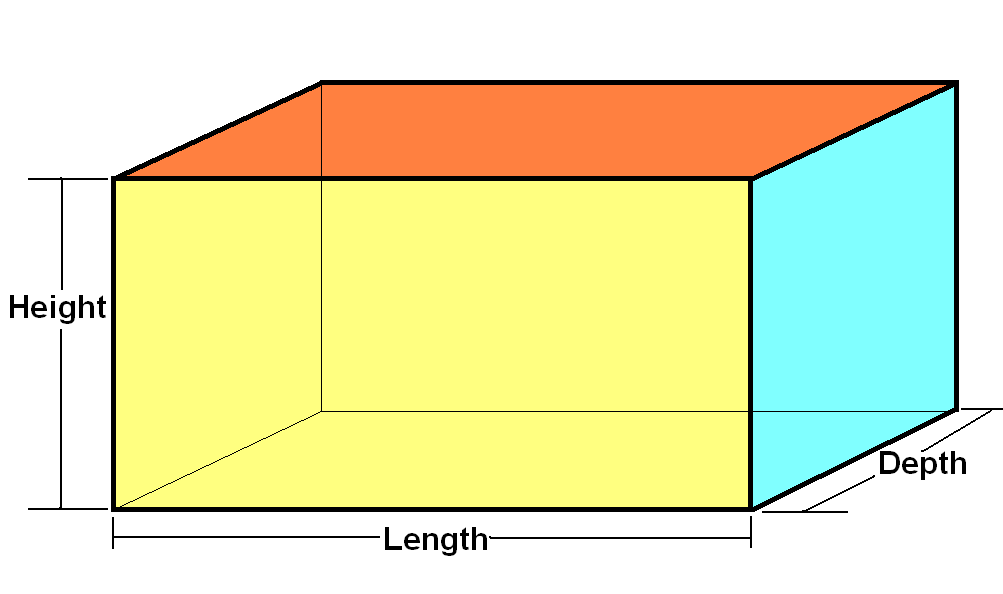
Using Type Synonyms
We can now use synonyms by creating values of the given types
circ0 :: CircleT
circ0 = (5, 1, 100) -- circle at (5,1) with radius 100
cub0 :: CuboidT
cub0 = (10, 20, 30) -- cuboid with l=10, d=20, h=30 And we can write functions over synonyms too
area :: CircleT -> Double
area (x, y, r) = pi * r * r
volume :: CuboidT -> Double
volume (l, d, h) = l * d * h We should get this behavior
>>> area circ0
31415.926535897932
>>> volume cub0
6000
QUIZ
Suppose we have the definitions
type CircleT = (Double, Double, Double)
type CuboidT = (Double, Double, Double)
circ0 :: CircleT
circ0 = (5, 1, 100) -- circle at (5,1) with radius 100
cub0 :: CuboidT
cub0 = (10, 20, 30) -- cuboid with length=10, depth=20, height=30
area :: CircleT -> Double
area (x, y, r) = pi * r * r
volume :: CuboidT -> Double
volume (l, d, h) = l * d * hWhat is the result of
>>> volume circ0A. 500
B. Type error
Answer: A
Beware!
Type Synonyms
Do not create new types
Just name existing types
And hence, synonyms
- Do not prevent confusing different values
Algebraic Data Types
Type Synonyms: naming existing types [done]
Product Types: bundling things together
Sum Types: types with multiple variants
Recursive Types: types that contain themselves
Polymorphic Datatypes: datatypes with parameters
Creating New Data Types
We can avoid mixing up values by creating new data types
-- | A new type `Circle` with constructor `MkCircle`,
-- which takes three arguments of type `Double`
data Circle = MkCircle Double Double Double
-- | A new type `Cuboid` with constructor `MkCuboid`
-- which takes three arguments of type `Double`
data Cuboid = MkCuboid Double Double DoubleWe use constructors to build values of the new type:
circ1 :: Circle
circ1 = MkCircle 5 1 100 -- circle at (5,1) w/ radius 100
cub1 :: Cuboid
cub1 = MkCuboid 10 20 30 -- cuboid w/ len=10, dep=20, ht=30
QUIZ
Suppose we create a new type with a data definition
-- | A new type `Circle` with constructor `MkCircle`
data Circle = MkCircle Double Double DoubleWhat is the type of the MkCircle constructor?
A. MkCircle :: Circle
B. MkCircle :: Double -> Circle
C. MkCircle :: Double -> Double -> Circle
D. MkCircle :: Double -> Double -> Double -> Circle
E. MkCircle :: (Double, Double, Double) -> Circle
Answer: D
Aside: Record syntax
Haskell’s record syntax allows you to name the constructor parameters:
Instead of
data Circle = MkCircle Double Double Doubleyou can write:
data Circle = MkCircle { center_x :: Double, center_y :: Double, radius :: Double }then you can do:
circ1 = MkCircle { center_x = 5, center_y = 1, radius = 100 } -- same as: circ1 = MkCircle 5 1 100 r = radius circ1 -- use field name as a function
QUIZ
Suppose we have the definitions
type CuboidT = (Double, Double, Double)
data Cuboid = MkCuboid Double Double Double
volume :: CuboidT -> Double
volume (l, d, h) = l * d * hWhat is the result of
>>> volume (MkCuboid 10 20 30)A. 6000
B. Type error
Answer: B
Deconstructing Data
Constructors let us build values of new type … but how to use those values?
How can we implement a function
volume :: Cuboid -> Double
volume c = ???such that
>>> volume (MkCuboid 10 20 30)
6000
Deconstructing Data by Pattern Matching
Haskell lets us deconstruct data via pattern-matching
volume :: Cuboid -> Double
volume (MkCuboid l d h) = l * d * h
area :: Circle -> Double
area (MkCircle x y r) = pi * r * rsame as for tuples, just using different constructors!
Algebraic Data Types
Type Synonyms: naming existing types [done]
Product Types: bundling things together [done]
Sum Types: types with multiple variants
Recursive Types: types that contain themselves
Polymorphic Datatypes: datatypes with parameters
Defining new types with data prevents us from mixing up values:
area :: Circle -> Double
area (MkCircle x y r) = pi * r * r
>>> area (MkCuboid 10 20 30) -- TYPE ERROR!But … what if we need to mix up values?
A List of Shapes
Suppose I need to represent a list of shapes
- Some
Circles - Some
Cuboids
What is the problem with shapes as defined below?
shapes = [circ1, cub1]Where we have defined
circ1 :: Circle
circ1 = MkCircle 5 1 100 -- circle at (5,1) with radius 100
cub1 :: Cuboid
cub1 = MkCuboid 10 20 30 -- cuboid with length=10, depth=20, height=30
This does not type-check!
All list elements must have the same type!
Solution?
Sum types
Lets create a single type that can represent both kinds of shapes!
data Shape
= MkCircle Double Double Double -- Circle at x, y with radius r
| MkCuboid Double Double Double -- Cuboid with length, depth, heightA sum type is a data type with multiple constructors
- aka enum in Rust
- aka (tagged) union in C
QUIZ
With the definition:
data Shape
= MkCircle Double Double Double -- Circle at x, y with radius r
| MkCuboid Double Double Double -- Cuboid with length, depth, heightWhat is the type of MkCircle 5 1 100 ?
A. Shape
B. Circle
C. MkCircle
D. (Double, Double, Double)
Answer: A
List of Shapes: Take 2
Now we can define
circ2 :: Shape
circ2 = MkCircle 5 1 100 -- circle at (5,1) with radius 100
cub2 :: Shape
cub2 = MkCuboid 10 20 30 -- cuboid with length=10, depth=20, height=30 and then define collections of Shapes
shapes :: [Shape]
shapes = [circ2, cub2]
2D Shapes
Lets define a type for 2D shapes
data Shape2D
= MkRect Double Double -- rectangle with width and height
| MkCirc Double -- circle with radius
| MkPoly [Vertex] -- polygon with at least three vertices
type Vertex = (Double, Double)Different constructors can have different types!
Tagged Boxes
A values of type Shape2D is either two doubles tagged with Rectangle
>>> :type (Rectangle 4.5 1.2)
(Rectangle 4.5 1.2) :: Shapeor a single double tagged with Circle
>>> :type (Circle 3.2)
(Circle 3.2) :: Shapeor a list of pairs of d tagged with Polygon
ghci> :type (Polygon [(1, 1), (2, 2), (3, 3)])
(Polygon [(1, 1), (2, 2), (3, 3)]) :: Shape

How do we get the value out of the box?
EXERCISE
Write a function to compute the perimeter of a Shape2D
data Shape2D = MkRect Double Double | MkCirc Double | MkPoly [Vertex]
type Vertex = (Double, Double)
perimeter :: Shape2D -> Double
perimeter s = ???HINT
You may want to use this helper that computes the distance between two points
distance :: Vertex -> Vertex -> Double
distance (x1, y1) (x2, y2) = sqrt ((x2 - x1) ** 2 + (y2 - y1) ** 2)
Algebraic Data Types
Type Synonyms: naming existing types [done]
Product Types: bundling things together [done]
Sum Types: types with multiple variants [done]
Recursive Types: types that contain themselves
Polymorphic Datatypes: datatypes with parameters
Recursive types
Have we seen an example already where
- a value of type
T - contains another value of the same type
Tinside?
Yes, lists!
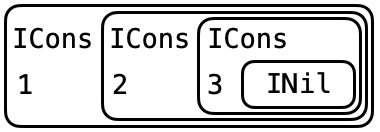
Lists aren’t built-in! They are an algebraic data type like any other:
data IntList
= INil -- empty list
-- ^ base constructor
| ICons Int IntList -- list with Int head and IntList tail
-- ^ inductive constructor (contains another IntList)
QUIZ
data IntList
= INil -- empty list
| ICons Int IntList -- list with Int head and IntList tailWhat is the type of ICons ?
A. IntList
B. Int -> IntList
C. (Int, IntList)
D. Int -> IntList -> IntList
E. IntList -> IntList
Answer: D
EXERCISE
With the definition:
data IntList = INil | ICons Int IntListWrite down an IntList representation of the list [1,2,3]
list_1_2_3 :: IntList
list_1_2_3 = ???
Recursion means boxes within boxes
Functions on recursive types
Recursive code mirrors recursive data
data IntList
= INil -- base constructor
| ICons Int IntList -- inductive constructorStep 1: add a pattern per constructor
length :: IntList -> Int
length INil = ... -- base case
length (ICons x xs) = ... -- recursive caseStep 2: fill in base case:
length :: IntList -> Int
length INil = 0
length (ICons x xs) = ...Step 3: fill in inductive case using a recursive call:
length :: IntList -> Int
length INil = 0
length (ICons x xs) = 1 + length xs
-- ^ recursive call on the "nested box"
EXERCISE: Append
Write an append function that appends two IntLists:
data IntList = INil | ICons Int IntList
append :: IntList -> IntList -> IntList
append = ???so that we can call:
-- [1,2] ++ [3,4] ==> [1,2,3,4]
>>> append (ICons 1 (ICons 2 INil)) (ICons 3 (ICons 4 INil))
(ICons 1 (ICons 2 (ICons 3 (ICons 4 INil))))
append :: List -> List -> List
append Nil ys = ys
append (Cons x xs) ys = Cons x (append xs ys)
Lessons Learned
- Recursive code mirrors recursive data
- With multiple arguments of a recursive type, which one should I recurse on?
- The name of the game is to pick the right inductive strategy!
Trees
Lists are unary trees:
How do we represent binary trees?
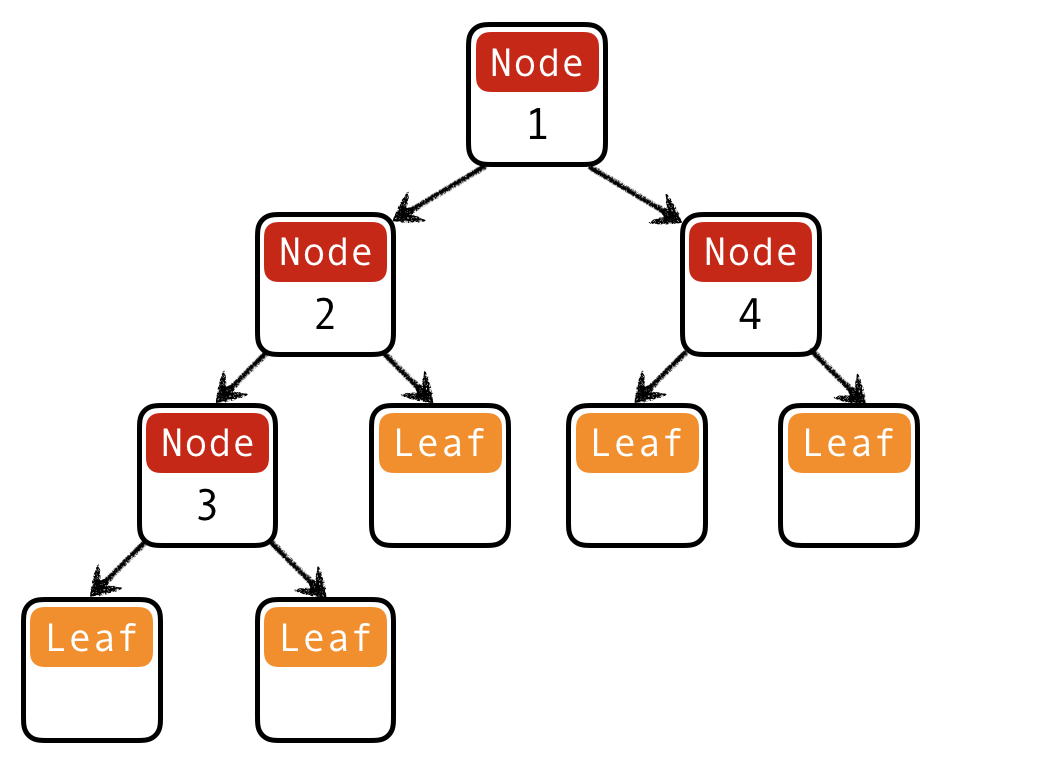
QUIZ: Binary trees
How do you represent this binary tree as a recursive datatype?

(A) data ITree = ILeaf | INode Int ITree
(B) data ITree = ILeaf | INode ITree ITree
(C) data ITree = ILeaf | INode Int ITree ITree
(D) data ITree = ILeaf Int | INode ITree ITree
(E) data ITree = ILeaf Int | INode Int ITree ITree
Answer: C

-- | Binary tree of integers
data ITree = ILeaf | INode Int ITree ITree
t1234 = INode 1
(INode 2 (INode 3 ILeaf ILeaf) ILeaf)
(INode 4 ILeaf ILeaf)
Functions on trees
height :: Tree -> Int
height Leaf = 0
height (Node _ l r) = 1 + max (height l) (height r)
Example: Calculator
I want to implement an arithmetic calculator to evaluate expressions like:
4.0 + 2.93.78 – 5.92(4.0 + 2.9) * (3.78 - 5.92)
What is a Haskell datatype to represent these expressions?
data Expr = ???
data Expr = Num Float
| Add Expr Expr
| Sub Expr Expr
| Mul Expr Expr
EXERCISE: Eval
With expressions defined as follows:
data Expr = Num Float
| Add Expr Expr
| Sub Expr Expr
| Mul Expr Exprwrite a function to evaluate an expression
eval :: Expr -> Float
eval (Num f) = f
eval (Add e1 e2) = eval e1 + eval e2
eval (Sub e1 e2) = eval e1 - eval e2
eval (Mul e1 e2) = eval e1 * eval e2
Algebraic Data Types
Type Synonyms: naming existing types [done]
Product Types: bundling things together [done]
Sum Types: types with multiple variants [done]
Recursive Types: types that contain themselves [done]
Polymorphic Datatypes: datatypes with parameters
Parameterized Types
Our IntList datatype can only store Ints :-(
What if we want to store Chars or Doubles?
data CharList
= CNil
| CCons Char CharList
data DoubleList
= DNil
| DCons Char DoubleList
Don’t Repeat Yourself!
Don’t repeat definitions - Instead reuse the list structure across all types!
Find abstract data patterns by
- identifying the different parts and
- refactor those into parameters
A Refactored List
Here are the three types: What is common? What is different?
data IList = INil | ICons Int IList
data CList = CNil | CCons Char CList
data DList = DNil | DCons Double DList
Common: Nil/Cons structure
Different: type of each “head” element
Refactored using Type Parameter
-- | A list of elements of type `a`
data List a = Nil | Cons a (List a)We can recover original types as instances of List:
iList :: List Int -- list where 'a' = 'Int'
iList = Cons 1 (Cons 2 (Cons 3 Nil))
cList :: List Char -- list where 'a' = 'Char'
cList = Cons 'a' (Cons 'b' (Cons 'c' Nil))
dList :: List Double -- list where 'a' = 'Double'
dList = Cons 1.1 (Cons 2.2 (Cons 3.3 Nil))
QUIZ
data List a = Nil | Cons a (List a)What is the type of Cons ?
A. Int -> List -> List
B. Int -> List Int -> List Int
C. Char -> List Char -> List Char
D. a -> List -> List
E. a -> List a -> List a
Answer: E
Type Constructors
Note: List is not a type!
List a, List Int, … are types
a is a type parameter
Then what is List?
A type-constructor that
- takes as input a type
a - returns as output the type
List a
Polymorphic Data has Polymorphic Constructors
Look at the types of the constructors
>>> :type Nil
Nil :: List aThat is, Nil is a value of any kind of list, and
>>> :type Cons
Cons :: a -> List a -> List aCons takes an a and a List a and returns a List a.
Polymorphic Functions
Let us refactor the append function to work on Lists:
data List a = Nil | Cons a (List a)append :: ??? -- What is the type of `append`?
append = ???
Polymorphic Functions over Polymorphic Data
The append function on Lists is polymorphic:
append :: List a -> List a -> List a
append Nil ys = ys
append (Cons x xs) ys = Cons x (append xs ys)append doesn’t care about the actual values in the list
- only manipulates the structure of the list
Hence append :: List a -> List a -> List a
- we can call
appendon lists of any kind - as long as both lists are of the same kind
>>> append (Cons 1 (Cons 2 Nil)) (Cons 3 Nil) -- a = Int
Cons 1 (Cons 2 (Cons 3 Nil))
>>> append (Cons 'a' (Cons 'b' Nil)) (Cons 'c' Nil) -- a = Char
Cons 'a' (Cons 'b' (Cons 'c' Nil))
QUIZ
With the type of append defined as
append :: List a -> List a -> List a
what would be result of
append (Cons 'a' (Cons 'b' Nil)) (Cons True Nil)A. Cons 'a' (Cons 'b' (Cons True Nil))
B. Cons 'a' (Cons 'b' Nil)
C. Type error
Answer: C
Built-in Lists?
This is exactly how Haskell’s “built-in” lists are defined:
data [a] = [] | (:) a [a]
data List a = Nil | Cons a (List a)Nilis called[]Consis called:
Many list manipulating functions e.g. in Data.List are polymorphic
- Can be reused across all kinds of lists.
(++) :: [a] -> [a] -> [a]
head :: [a] -> a
tail :: [a] -> [a]
That’s all folks!
