Last Week

The interpreter:

• How do we evaluate a program given its abstract syntax tree (AST)?

Next two Weeks

Modern language features for structuring programs

• Type classes
• Monads

that will help us add cool features to the Nano interpreter!

Type Classes: Outline

1. Why type classes?
2. Standard type classes
3. Creating new instances
4. Typeclasses and Polymorphism
5. Creating new type classes

Overloading Operators: Arithmetic

The + operator works for a bunch of different types.

For Integer:

λ> 2 + 3
5

for Double precision floats:

λ> 2.9 + 3.5
6.4

Overloading Comparisons

Similarly we can compare different types of values

λ> 2 == 3
False

λ>  [2.9, 3.5] == [2.9, 3.5]
True

λ> ("cat", 10) < ("cat", 2)
False

λ> ("cat", 10) < ("cat", 20)
True

Operator Overloading

Seems unremarkable?

Languages have supported “operator overloading” since the dawn of time

Haskell has no caste system

No distinction between operators and functions

• All are first class citizens!

You can implement functions like (+) and (==) yourself from scratch!

• But then, what type do we give them?

QUIZ

Which of the following type annotations would work for (+) ?

(A) (+) :: Int -> Int -> Int

(B) (+) :: Double -> Double -> Double

(C) (+) :: a -> a -> a

(D) Any of the above

(E) None of the above

Int -> Int -> Int is bad because?

• Then we cannot add Doubles!

Double -> Double -> Double is bad because?

• Then we cannot add Ints!

a -> a -> a is bad because?

• I don’t know how to implement this

• For some as it doesn’t make sense: how do I add two Bools? Or two Chars?

Ad-hoc Polymorphism

We have seen parametric polymorphism:

-- Append two lists:
(++) :: [a] -> [a] -> [a]
(++) []     ys = ys
(++) (x:xs) ys = x:(xs ++ ys)

(++) works for all list types

• Doesn’t care what the list elements are

• The same implementation works for a = Int, a = Bool, etc.

Now we need ad-hoc polymorphism:

(+) :: a -> a -> a -- Almost, but not really
(+) x y = ???

(+) should work for many (but not all) types

• Different implementation for a = Int, a = Double, etc.

Ad-hoc means “created or done for a particular purpose as necessary.”

Type Classes for Ad Hoc Polymorphism

Haskell solves this problem with a mechanism called type classes

• Introduced by Wadler and Blott

This is a very cool and well-written paper! Read it!

Constrained Types

Let’s ask GHCi:

λ> :type (+)
(+) :: (Num a) => a -> a -> a

We call this a constrained (or qualified) type

Read it as:

• (+) takes in two a values and returns an a value

• for any type a that

• is an instance of the Num type class

• or, in Java terms: implements the Num interface

• similar but not the same idea!

The “(Num a) =>” part is called the constraint

Some types are Nums:

• For example, Int, Integer, Double
• Values of those types can be passed to (+):

λ> 2 + 3
5

Other types are not Nums:

• For example, Bool, Char, String, function types, …
• Values of those types cannot be passed to (+):

λ> True + False

<interactive>:15:6:
    No instance for (Num Bool) arising from a use of ‘+’
    In the expression: True + False
    In an equation for ‘it’: it = True + False

Aha! Now those no instance for error messages should make sense!

• Haskell is complaining that True and False are of type Bool
• and that Bool is not an instance of Num

QUIZ

What would be a reasonable type for the equality operator?

(A) (==) :: a -> a -> a

(B) (==) :: a -> a -> Bool

(C) (==) :: (Eq a) => a -> a -> a

(D) (==) :: (Eq a) => a -> a -> Bool

(E) None of the above

Type Classes: Outline

1. Why type classes? [done]
2. Standard type classes
3. Creating new instances
4. Typeclasses and Polymorphism
5. Creating new type classes

What is a type class?

A type class is a collection of methods (functions, operations) that must exist for every instance

What are some useful type classes in the Haskell standard library?

The Eq Type Class

The simplest typeclass is Eq:

class  Eq a  where
  (==) :: a -> a -> Bool
  (/=) :: a -> a -> Bool

A type T is an instance of Eq if there are two functions

• (==) :: T -> T -> Bool that determines if two T values are equal
• (/=) :: T -> T -> Bool that determines if two T values are disequal

Lifehack: You can ask GHCi about a type class and it will tell you

• its methods
• all the instances it knows

λ> :info Eq
class  Eq a  where
  (==) :: a -> a -> Bool
  (/=) :: a -> a -> Bool
...
instance Eq Int
instance Eq Double
...

The Ord Typeclass

The type class Ord is for totally ordered values:

class Eq a => Ord a where
  (<)  :: a -> a -> Bool
  (<=) :: a -> a -> Bool
  (>)  :: a -> a -> Bool
  (>=) :: a -> a -> Bool

For example:

λ> 2 < 3
True

λ> "cat" < "dog"
True

Note Eq a => in the class definition!

A type T is an instance of Ord if

1. T is also an instance of Eq, and
2. It defines functions for comparing values for inequality

The Num Type Class

The type class Num requires that instances define a bunch of arithmetic operations

class Num a where
  (+) :: a -> a -> a
  (-) :: a -> a -> a
  (*) :: a -> a -> a
  negate :: a -> a
  abs :: a -> a
  signum :: a -> a
  fromInteger :: Integer -> a

The Show Type Class

The type class Show requires that instances be convertible to String

class Show a  where
  show :: a -> String

Indeed, we can test this on different (built-in) types

λ> show 2
"2"

λ> show 3.14
"3.14"

λ> show (1, "two", ([],[],[]))
"(1,\"two\",([],[],[]))"

The Read Typeclass

-- Not the actual definition, but almost:
class Read a where
  read :: String -> a

Read is the opposite of Show

• It requires that every instance T can parse a string and turn it into T

• Just like with Show, most standard type are instances of Read:

  • Int, Integer, Double, Char, Bool, etc

QUIZ

What does the expression read "2" evaluate to?

(A) Type error

(B) "2"

(C) 2

(D) 2.0

(E) Run-time error

Haskell is foxed!

• Doesn’t know what type to convert the string to!
• Doesn’t know which of the read functions to run!

Did we want an Int or a Double or maybe something else altogether?

Thus, here an explicit type annotation is needed to tell Haskell what to convert the string to:

λ> (read "2") :: Int
2

λ> (read "2") :: Float
2.0

λ> (read "2") :: String
???

Note the different results due to the different types.

Standard Typeclass Hierarchy

Haskell comes equipped with a rich set of built-in classes.

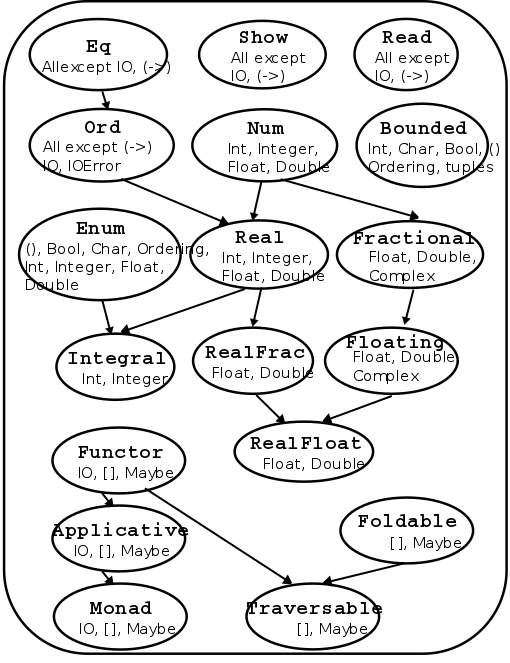
In the above picture, there is an edge from Eq to Ord because for something to be an Ord it must also be an Eq.

Type Classes: Outline

1. Why type classes? [done]
2. Standard type classes [done]
3. Creating new instances
4. Typeclasses and Polymorphism
5. Creating new type classes

Showing Your Colors

Let’s create a new datatype:

data Color = Red | Green

and play with it in GHCi:

λ> let col = Red
λ> :type col
x :: Color

So far, so good… but we cannot view them!

λ> col

<interactive>:1:0:
    No instance for (Show Color)
      arising from a use of `print' at <interactive>:1:0
    Possible fix: add an instance declaration for (Show Color)
    In a stmt of a 'do' expression: print it

Why is this happening?

When we type an expression into GHCi it:

1. evaluates it to a value, then
2. calls show on that value to convert it to a string

But our new type is not an instance of Show!

We also cannot compare colors!

λ> col == Green

<interactive>:1:0:
    No instance for (Eq Color)
      arising from a use of `==' at <interactive>:1:0-5
    Possible fix: add an instance declaration for (Eq Color)
    In the expression: col == Green
    In the definition of `it': it = col == Green

How do we add an instance declaration for Show Color and Eq Color?

Creating Instances

To tell Haskell how to show or compare values of type Color

• create instances of Eq and Show for that type:

instance Show Color where
  show Red   = "Red"
  show Green = "Green"

instance Eq Color where
  ???

EXERCISE: Creating Instances

Create an instance of Eq for Color:

data Color = Red | Green

instance Eq Color where
  ???

-- Reminder:
class  Eq a  where
  (==) :: a -> a -> Bool
  (/=) :: a -> a -> Bool

QUIZ

Which of the following Eq instances for Color are valid?

-- (A)
instance Eq Color where
  (==) Red   Red   = True
  (==) Green Green = True
  (==) _     _     = False

-- (B)
instance Eq Color where
  (/=) Red   Red   = False
  (/=) Green Green = False
  (/=) _     _     = True

-- (C) Neither of the above

-- (D) Either of the above

Default Method Implementations

The Eq class is actually defined like this:

class  Eq a  where
  (==) :: a -> a -> Bool
  (==) x y = not (x /= y) -- Default implementation!

  (/=) :: a -> a -> Bool
  (/=) x y = not (x == y) -- Default implementation!

The class provides default implementations for its methods

• An instance can define any of the two methods and get the other one for free

• Use :info to find out which methods you have to define:

λ> :info Eq
class  Eq a  where
  (==) :: a -> a -> Bool
  (/=) :: a -> a -> Bool
  {-# MINIMAL (==) | (/=) #-} -- HERE HERE!!!

QUIZ

If you define:

instance Eq Color where
  -- Nothing here!

what will the following evaluate to?

λ> Red == Green

(A) Type error

(B) Runs forever / stack overflow

(C) Other runtime error

(D) False

(E) True

Automatic Derivation

This is silly: we should be able to compare and view Colors “automatically”!

Haskell lets us automatically derive functions for some classes in the standard library.

To do so, we simply dress up the data type definition with

data Color = Red | Green
  deriving (Eq, Show) -- please generate instances automatically!

Now we have

λ> let col = Red

λ> col
Red

λ> col == Red
True

Type Classes: Outline

1. Why type classes? [done]
2. Standard type classes [done]
3. Creating new instances [done]
4. Typeclasses and Polymorphism
5. Creating new type classes

Let’s build a small library for dictionaries mapping keys k to values v

data Dict k v
  = Empty                -- empty dictionary
  | Bind k v (Dict k v)  -- bind key `k` to the value `v`
  deriving (Show)

The API

We want to be able to do the following with Dict:

>>> let dict0 = add "cat" 10.0 (add "dog" 20.0 empty)

>>> get "cat" dict0
10

>>> get "dog" dict0
20

>>> get "horse" dict0
error: key not found

Okay, lets implement!

-- | 'add key val dict' returns a new dictionary
-- | that additionally maps `key` to `val`
add :: k -> v -> Dict k v -> Dict k v
add key val dict = ???

-- | 'get key dict' returns the value of `key`
get :: k -> Dict k v -> v
get key dict = ???

But we get a type error!

Constraint Propagation

Lets delete the types of add and get and see what Haskell says their types are!

λ> :type get
get :: (Eq k) => k -> v -> Dict k v -> Dict k v

Haskell tells us that we can use any k type as a key as long as this type is an instance of the Eq typeclass.

How, did GHC figure this out?

• If you look at the code for get you’ll see that we check if two keys are equal!

EXERCISE: A Faster Dictionary

Write an optimized version of

• add that ensures the keys are in increasing order
• get that gives up the moment we see a key that’s larger than the one we’re looking for

(How) do you need to change the types of get and add?

Type Classes: Outline

1. Why type classes? [done]
2. Standard type classes [done]
3. Creating new instances [done]
4. Typeclasses and Polymorphism [done]
5. Creating new type classes

Creating Typeclasses

Typeclasses are useful for many different things

• Improve readability
• Promote code reuse

We will see some very interesting use cases over the next few lectures.

Lets conclude today’s class with a quick example that provides a taste.

Dictionary with Default Values

Recall that our get function throws an error when the key is not found:

get key Empty      = error "key not found"
get key (Bind oldK v rest)
  | key == oldK    = v
  | key < oldK     = error "key not found"
  | otherwise      = get key rest

Let’s modify our implementation of fast dictionaries so that get returns a default value instead:

λ> get 2       (add 5 "five"   (add 10 "ten"  (add 3 "three" Empty)))
""

λ> get "horse" (add "cat" 10.0 (add "dog" 20.1 Empty))
0.0

How can we achieve this?

Option 1: add an argument to get

get def key Empty = def
get def key (Bind oldK v rest)
  | key < oldK     = def
  | ...

But then the client has to do:

λ> let dict = add 5 "five"   (add 10 "ten"  (add 3 "three" Empty))
λ> get "" 2 dict
""
-- Need to pass in an extra argument every time! annoying!
λ> get "" 5 dict
"five"

Option 2: store the default value in the dictionary

data Dict k v
  = Empty v               -- store the default value here
  | Bind k v (Dict k v) v -- and maybe also here

Limitations?

Type Classes to the Rescue!

Would it be too much to ask for a magical defValue…

get def key Empty = defValue
get def key (Bind oldK v rest)
  | key < oldK    = defValue
  | ...

… which has different values depending on the type of v?

λ> get 2       (add 5 "five"   (add 10 "ten"  (add 3 "three" Empty)))
"" -- default value for strings

λ> get "horse" (add "cat" 10.0 (add "dog" 20.1 Empty))
0.0 -- default value for floats

That’s what type classes are for!

-- (<) is a magical function
-- with different implementations depending on the argument type:
λ> 1 < 2
True

λ> "cat" < "dog"
True

Type Class for Default Values

class Default a where
  defValue :: a

Now we need to tell get that v has a default value:

get :: (Ord k, Default v) => k -> Dict k v -> v
get key Empty = defValue -- uses the method of the Default class!
get key (Bind oldK v rest)
  | key < oldK    = defValue
  | key == oldK   = v
  | otherwise     = get key rest

Finally, we need to define instances of Default for different value types:

instance Default Int where
  defValue = 0

instance Default [a] where
  defValue = []

That’s all folks!