cse130

Parsers

A parser is a function that

converts unstructured data (e.g. String, array of Byte,…)
into structured data (e.g. JSON object, Markdown, AST…)

type Parser = String -> StructuredObject

Every large software system contains a Parser

System	Parses
Compiler	Source code
Shell Scripts	Command-line options
Database	SQL queries
Web Browser	HTML, CSS, JS, …
Games	Level descriptors
Routers	Packets

How to build Parsers?

Two standard methods

Regular Expressions

Doesn’t really scale beyond simple things
No nesting, recursion

Parser Generators

Specify grammar via rules

Expr : Var            { EVar $1       }
     | Num            { ENum $1       }
     | Expr Op Expr   { EBin $1 $2 $3 }
     | '(' Expr ')'   { $2            }
     ;

Tools like yacc, bison, antlr, happy

convert grammar into executable function

Grammars Don’t Compose!

If we have two kinds of structured objects Thingy and Whatsit.

Thingy : rule 	{ action }
;

Whatsit : rule  { action }
;

To parse sequences of Thingy and Whatsit we must repeat ourselves:

Thingies : Thingy Thingies  { ... }
           EmptyThingy      { ... }
;

Whatsits : Whatsit Whatsits { ... }
           EmptyWhatsit     { ... }
;

No way to:

Define a generic parser for sequences
Reuse this generic parser for Thingy and Whatsit

A New Hope: Parsers as Functions

Lets think of parsers directly as functions that

Take as input a String
Convert a part of the input into a StructuredObject
Return the remainder unconsumed to be parsed later

data Parser a = P (String -> (a, String))

A Parser a

Converts a prefix of a String
Into a structured object of type a and
Returns the suffix String unchanged

Parsers Can Produce Many Results

Sometimes we want to parse a String like

"2 + 3 + 4"

into a list of possible results

[(Plus (Plus 2 3) 4),   Plus 2 (Plus 3 4)]

So we generalize the Parser type to

data Parser a = P (String -> [(a, String)])

Running a Parser

Given the definition

data Parser a = P (String -> [(a, String)])

how should we implement?

runParser :: Parser a -> String -> [(a, String)]
runParser p s = ???

runParser :: Parser a -> String -> [(a, String)]
runParser (P f) s = f s

QUIZ

Given the definition

data Parser a = P (String -> [(a, String)])

Which of the following is a valid oneChar :: Parser Char

that returns the first Char from a string (if one exists)

-- A
oneChar = P (\s -> head s)

-- B
oneChar = P (\s -> case s of
                      []   -> [('', s)]
                      c:cs -> [c, cs])

-- C
oneChar = P (\s -> (head s, tail s))

-- D
oneChar = P (\s -> [(head s, tail s)])

-- E
oneChar = P (\s -> case s of
                      [] -> []
                      c:cs -> [(c, cs)])

Lets Run Our First Parser!

>>> runParser oneChar "hey!"
[('h', "ey")]

>>> runParser oneChar "yippee"
[('y', "ippee")]

>>> runParser oneChar ""
[]

Failure to parse means result is an empty list!

EXERCISE

Your turn: Write a parser to grab first two chars

twoChar :: Parser (Char, Char)
twoChar = P (\cs -> ???)

When you are done, we should get

>>> runParser twoChar "hey!"
[(('h', 'e'), "y!")]

>>> runParser twoChar ""
[]

>>> runParser twoChar "h"
[]

Composing Parsers

We can write twoChars from scratch like so:

twoChar :: Parser (Char, Char)
twoChar  = P (\cs -> case cs of
                       c1:c2:cs' -> [((c1, c2), cs')]
                       _         -> [])

But this is sad: would be much better to reuse oneChar!

twoChar :: Parser (Char, Char)
twoChar = pairP oneChar oneChar

QUIZ

twoChar :: Parser (Char, Char)
twoChar = pairP oneChar oneChar

What must the type of pairP be?

A. Parser (Char, Char)

B. Parser Char -> Parser (Char, Char)

C. Parser a -> Parser a -> Parser (a, a)

D. Parser a -> Parser b -> Parser (a, b)

E. Parser a -> Parser (a, a)

A Pair Combinator

Lets implement pairP!

pairP :: Parser a -> Parser b -> Parser (a, b)
pairP aP bP = ???

High-level idea:

Run aP on the input string
For each result (a, s') of aP, run bP on s'
For each result (b, s'') of bP, return ((a, b), s'')

-- | We have just seen this "for-each" function in the previous lecture!
forEach :: [a] -> (a -> [b]) -> [b]
forEach xs f = concatMap f xs

pairP :: Parser a -> Parser b -> Parser (a, b)
pairP aP bP = P (\s -> forEach (runParser aP s)  (\(a, s') ->
                       forEach (runParser bP s') (\(b, s'') ->
                       [((a, b), s'')])
                ))

This works, but is was a bit of a pain to write!

Does this code look familiar?

It’s like doing mutable state + non-determinism the hard way!

i.e. without monads

Also, take a second look at the Parser type:

data Parser a = P (String -> [(a, String)])

data State s a   = S (s -> (a, s))

Parser is a Monad!

Like State and [], Parser is a monad!

We need to implement two functions

returnP :: a -> Parser a

bindP   :: Parser a -> (a -> Parser b) -> Parser b

QUIZ

Which of the following is a valid implementation of returnP

data Parser a = P (String -> [(a, String)])

returnP   :: a -> Parser a

returnP a = P (\s -> [])          -- A

returnP a = P (\s -> [(a, s)])    -- B

returnP a = P (\s -> (a, s))      -- C

returnP a = P (\s -> [(a, "")])   -- D

returnP a = P (\s -> [(s, a)])    -- E

HINT: what did return do for State and []?

Bind for Parsers

Next, lets implement bindP

bindP :: Parser a -> (a -> Parser b) -> Parser b
bindP aP fbP = ???

High-level idea:

Run aP on the input string
For each result (a, s') of aP, run bp = fbP a on s'
For each result (b, s'') of bP, return (b, s'')

In other words, this is just a generalization of pairP!

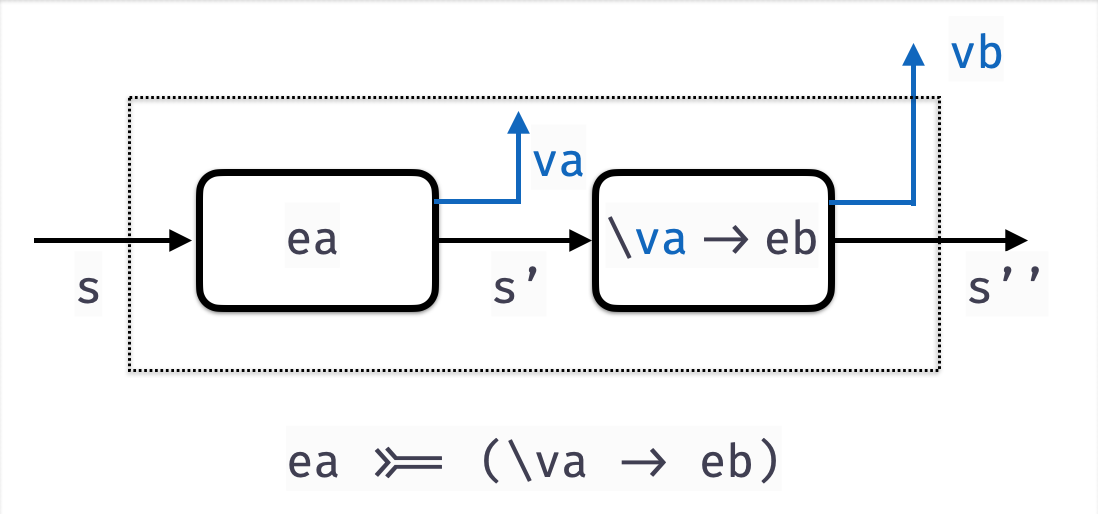
bindP :: Parser a -> (a -> Parser b) -> Parser b
bindP aP fbP = P (\s ->
  forEach (runParser aP s) (\(a, s') ->
    forEach (runParser (fbP a) s') (\(b, s'') ->
      [(b, s'')]
    )
  )
)

The Parser Monad

We can now make Parser an instance of Monad

instance Monad Parser where
  (>>=)  = bindP
  return = returnP

And now, let the wild rumpus begin!

Parser Combinators

Lets write lots of high-level operators to combine parsers!

Here’s a cleaned up pairP

pairP :: Parser a -> Parser b -> Parser (a, b)
pairP aP bP = do
  a <- aP
  b <- bP
  return (a, b)

Failures are the Pillars of Success!

Surprisingly useful, always fails

i.e. returns [] no successful parses

failP :: Parser a
failP = P (\_ -> [])

QUIZ

Consider the parser

satP :: (Char -> Bool) -> Parser Char
satP p = do
  c <- oneChar
  if p c then return c else failP

What is the value of

quiz1 = runParser (satP (\c -> c == 'h')) "hello"
quiz2 = runParser (satP (\c -> c == 'h')) "yellow"

	`quiz1`	`quiz2`
A	`[]`	`[]`
B	`[('h', "ello")]`	`[('y', "ellow")]`
C	`[('h', "ello")]`	`[]`
D	`[]`	`[('y', "ellow")]`

Parsing Alphabets and Numerics

We can now use satP to write

-- parse ONLY the Char c
charP :: Char -> Parser Char
charP c = satP (\c' -> c == c')

-- parse ANY ALPHABET
alphaCharP :: Parser Char
alphaCharP = satP isAlpha

-- parse ANY NUMERIC DIGIT
digitCharP :: Parser Char
digitCharP = satP isDigit

QUIZ

We can parse a single Int digit

digitP :: Parser Int
digitP = do
  c <- digitCharP     -- parse the Char c
  return (read [c])   -- convert Char to Int

What is the result of

quiz1 = runParser digitP "92"
quiz2 = runParser digitP "cat"

	`quiz1`	`quiz2`
A	`[]`	`[]`
B	`[('9', "2")]`	`[('c', "at")]`
C	`[(9, "2")]`	`[]`
D	`[]`	`[('c', "at")]`

A Choice Combinator

Lets write a combinator p1 <|> p2 that

returns the results of p1

or, else if those are empty

returns the results of p2

E.g. <|> lets us build a parser that produces an alphabet OR a numeric character

alphaNumCharP :: Parser Char
alphaNumCharP = alphaCharP <|> digitCharP

Which should produce

>>> runParser alphaNumCharP "cat"
[('c', "at")]

>>> runParser alphaNumCharP "2cat"
[('2', "cat")]

QUIZ

(<|>) :: Parser a -> Parser a -> Parser a
p1 <|> p2 = ??? -- produce results of `p1` if non-empty
                -- OR-ELSE results of `p2`

Which of the following implements (<|>)?

do -- (A)
  r1s <- p1
  r2s <- p2
  return (r1s ++ r2s)

do -- (B)
  r1s <- p1
  case r1s of
    [] -> p2
    _  -> return r1s

-- (C)
P (\s -> runParser p1 s ++ runParser p2 s)

-- (D)
P (\s ->
  case runParser p1 s of
    []  -> runParser p2 s
    r1s -> r1s
  )

A Simple Expression Parser

Let’s write a parser expr :: Parser Int that parses and evaluates simple arithmetic expressions

an expression is a + b, a - b, a * b, a / b
where a and b are single-digit integers

>>> runParser expr "8/2"
[(4,"")]

>>> runParser expr "8+2cat"
[(10,"cat")]

>>> runParser expr "8-2cat"
[(6,"cat")]

>>> runParser expr "8*2cat"
[(16,"cat")]

-- 1. First, parse the operator
opP      :: Parser (Int -> Int -> Int)
opP      = plus <|> minus <|> times <|> divide
  where
    plus   = do { _ <- charP '+'; return (+) }
    minus  = do { _ <- charP '-'; return (-) }
    times  = do { _ <- charP '*'; return (*) }
    divide = do { _ <- charP '/'; return div }

-- 2. Now parse the expression!
expr :: Parser Int
expr = do x  <- digitP
          op <- opP
          y  <- digitP
          return (x `op` y)

QUIZ

What will quiz evaluate to?

expr :: Parser Int
expr = do x  <- digitP
          op <- opP
          y  <- digitP
          return (x `op` y)

quiz = runParser expr "10+2"

A. [(12,"")]

B. []

C. [(10, "+2")]

D. [(1, "0+2")]

E. Run-time exception

Next: Recursive Parsing

Its cool to parse individual Char …

… but way more interesting to parse recursive structures!

"((2 + 10) * (7 - 4)) * (5 + 2)"

EXERCISE: Parsing Many Times

Often we want to repeat parsing some object

E.g. to parse an Int we need to parse a digit many times

Implement a function manyP that:

applies a parser p as many times as it can
returns a list of the results

-- | `manyP p` repeatedly runs `p` to return a list of [a]
manyP  :: Parser a -> Parser [a]
manyP = ???

>>> runParser (manyP digitCharP) "2022cat"
[("2022","cat")]

>>> runParser (manyP digitCharP) "cat"
[("","cat")]

-- | `manyP p` repeatedly runs `p` to return a list of [a]
manyP  :: Parser a -> Parser [a]
manyP p = m1 <|> m0
  where
    m0  = return []
    m1  = do { x <- p; xs <- manyP p; return (x:xs) }

Parsing at least one

Often we need to parse at least one repetition:

manyOneP :: Parser a -> Parser [a]
manyOneP p = do { x <- p; xs <- manyP p; return (x:xs) }

Parsing Numbers

Now, we can write a parser for natural numbers:

int :: Parser Int
int = do { xs <- manyOneP digitChar; return (read xs) }

>>> runParser int "2022cat"
[(2022,"cat")]

>>> runParser int "cat"
[] -- parser fails, as expected!

Parsing Arithmetic Expressions

Now we can build a proper calculator!

expr ::  Parser Int
expr = binExp <|> int

binExp :: Parser Int
binExp = do
  x <- int
  o <- opP
  y <- expr
  return (x `o` y)

Works pretty well!

>>> runParser expr "11+22+33"
[(66,"")]

>>> runParser expr "11+22-33"
[(0,"")]

WARNING

The real (<|>) combinator in Parsec has different semantics:

It only runs p2 if p1 fails without consuming any input

This makes parsers more efficient
And helps with error reporting

To choose between objects that can have the same prefix, you need to use try:

-- In Parsec
expr ::  Parser Int
expr = try binExp <|> int

Otherwise, runParser expr "10" would fail

because binExp consumes the 10
so int is never tried

QUIZ

expr ::  Parser Int
expr = binExp <|> int

binExp :: Parser Int
binExp = do
  x <- int
  o <- opP
  y <- expr
  return (x `o` y)

What does quiz evaluate to?

quiz = runParser expr "10-5-5"

A. [(0, "")]

B. []

C. [(10, "")]

D. [(10, "-5-5")]

E. [(5, "-5")]

Problem: Right-Associativity

binExp :: Parser Int
binExp = do
  x <- int
  o <- opP
  y <- expr
  return (x `o` y)

"10-5-5" gets parsed as 10 - (5 - 5) because

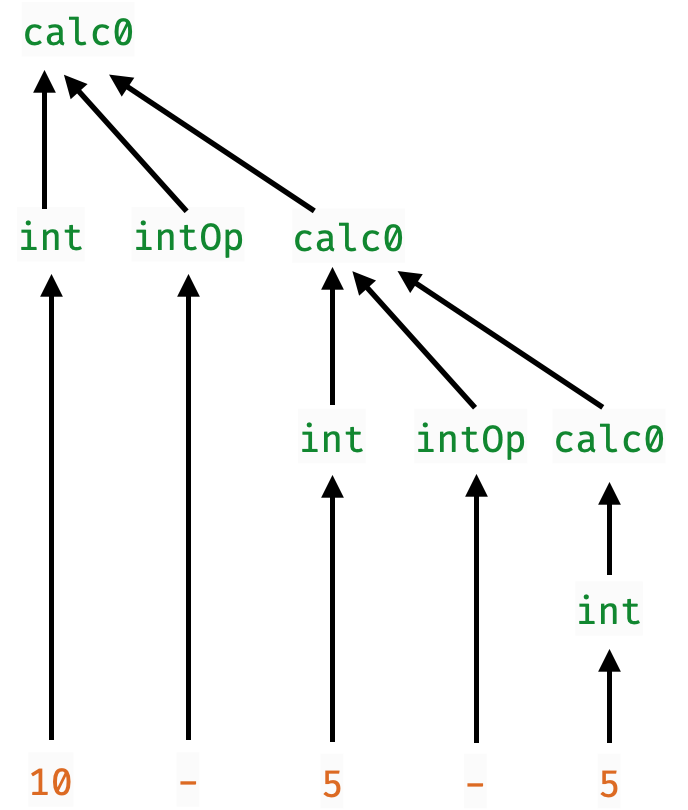
The expr parser implicitly forces each operator to be right associative

doesn’t matter for +, *
but is incorrect for -, div

Left-Associative Parsing

How can we make the parser left associative

i.e. parse “10-5-5” as (10 - 5) - 5 ?

Lets flip the order!

binExp :: Parser Int
binExp = do
  x <- expr -- now expr is on the left
  o <- intOp
  y <- int
  return (x `o` y)

But …

>>> runParser expr "2+2"
...

Infinite loop! expr --> binExp --> expr --> binExp --> ...

without consuming any input :-(

Instead of

expr :== int "-" (int "-" (... "-" (int "-" int)))

we want

expr :== (((int "-" int) "-" int) "-" ... "-" int)

Does this remind you of any standard computation patterns?

Fold right vs fold left!

Fold Left Parser

Lets implement foldLP aP oP as a combinator

vP parses a single a value
oP parses a binary operator a -> a -> a
foldLP vP oP parses and returns the result ((v1 o v2) o v3) o v4) o ... o vn)

But how?

grab the first v1 using vP
continue by
- either trying oP then v2 … and recursively continue with v1 o v2
- or else (no more o) just return v1

foldLP :: Parser a -> Parser (a -> a -> a) -> Parser a
foldLP vP oP = do {v1 <- vP; continue v1}
  where
    continue v1 = do { o <- oP; v2 <- vP; continue (v1 `o` v2) }
               <|> return v1

Now we can define

expr = foldLP int opP

Lets make sure it works!

>>> runParser expr "10-5-5"
[(0,"")]

QUIZ

expr = foldLP int opP

What is the value of

quiz1 = runParser expr "10*2+100"
quiz2 = runParser expr "100+10*2"

	`quiz1`	`quiz2`
A	`[]`	`[]`
B	`[120, "")]`	`[(120, "")]`
C	`[120, "")]`	`[(220, "")]`
D	`[1020, "")]`	`[(120, "")]`

Operator precedence

Our parser treats all operators at the same precendence level!

in reality, * and / should have higher precedence than + and -

Solution: Grammar Factoring

Any expression is a sum-of-products!

  expr :== (((prod "+" prod) "+" prod) "+" ... "+" prod)
  prod :== (((atom "*" atom) "*" atom) "*" ... "*" atom)
  atom :== "(" expr ")" | int

Or in Haskell:

expr = foldLP prod (plus <|> minus)
prod = foldLP atom (times <|> div)
atom = parensP expr <|> int

All that is left is to implement parensP!

EXERCISE: Parsing Parenthetic Expressions

Implement the function parensP:

-- | Parse what `p` parses, surrounded by parentheses:
parensP :: Parser a -> Parser a
parensP p = ???

>>> runParser (parensP int) "(10)"
[(10,"")]

>>> runParser (parensP int) "10"
[]

Lets make sure it works!

>>> runParser expr "10*2+100"
[(120,"")]

>>> runParser expr  "100+10*2"
[(120,"")]

>>> runParser expr  "(100+10)*2"
[(220,"")]

Parser combinators

That was a taste of Parser Combinators

Transferred from Haskell to many other languages.

Many libraries including Parsec used in your homework - oneOrMore is called chainl

Read more about the theory - in these recent papers

Read more about the practice - in this recent post that I like JSON parsing from scratch